"the platypus of physics"

subheading: imaginary solids
published title: impossible crystals
actual topic: quasicrystals
factual title: on tiles
Epilogue: to be continued

Introducing Hans Christian von Baeyer:


I've just read one of his stories in an Olaf Eliasson book called Surroundings Surrounded. Featuring:
Martin Gardner > Roger Penrose > M.C. Escher > Paul Steinhardt & Dov Levine > Robert Ammann > Fibonacci > David Nelson > Linus Pauling > George Onoda > Steinhardt again > the future.

It is so good I have applied a highlighter:

In 1977, Gardner asked his Scientific American readership how to cover a plane with tiles, with emphasis on the pentagon. I prefer to call it the fantom pentagon myself.

Fantom pentagon in aperiodic Penrose tiles:

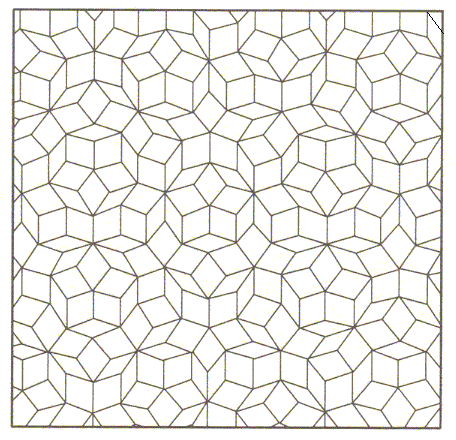
(fat diamond=interior angles of reg. pentagon, skinny diamond=interior angles of pentagon's diagonals)

Penrose first arranged these tiles a short time after 1974. This is where I should stop and point at this story which tells it properly. Maybe I will. But that's a bit lazy. Ok I'll carry on being lay-ms: for a few years after, people played with 3D aperiodic tiling, making polyhedra to fill imaginary space.

And then came the thought: atoms instead of tiles.
In 1984 Paul & Dov made a computer program to calculate the diffraction patterns these imaginary structures would produce, if they were atoms. It would look like this:

Fantom pentagon x-ray. Ni glass, ni crystal:


Which brings me to the classification of dots, to be applied to every pure solid in nature:

Fuzzy = glass, sharp = crystal.
Random= glass, periodic = crystal.

This is where Ammann, amateur mathematician superstar, comes in and explains how dots can be both sharp and periodic: quasiperiodicity! (it involves fivefold grids made using fibonacci-adjusted spaces between parallel lines. These Ammann lines are 2 lengths, the ratio between them being golden.)

We have now covered the sub-heading and published title.

Which brings us to the discovery of such a thing actually existing, in 1984 - an alloy of aluminium and manganese. Which cannot be theoretically explained. Or found on flickr.

Which leaves us with the epilogue.
In 1988 Onoda managed to grow perfect quasicrystals in tiles with a set of local rules. Hans finished his story here as the ideas don't stretch outwards, restricted as they are by the ever-dramatic forbidden symmetry, coined by Marjorie Senechal.

Introducing Marjorie Senechal:


Marjorie wrote What is a Quasicrystal and was a member of the International Union for Crystallography's Aperiodic Crystal Commission in 1992, when they added a PS to the definition of a crystal, whereby if “three dimensional lattice periodicity can be considered to be absent,” the crystal is aperiodic (quasiperiodic).

She highlights the current gap between the study of mathematical long-range aperiodicity, and scientific research into aperiodic crystals: the former gives us rotational symmetry of any finite order, and the latter: pentagonal, decagonal, dodecagonal and icosahedral only. And insists that the term quasiperiodic (aperiodic) is not a cop-out. And finishes her paper with the words Stay tuned. Which is a cop-out.

Now I want to go to the APS meeting in March: Session D27: Fullerenes, Nano-membranes, and Quasicrystals.
You think they need an illustrator?